无标题无名氏No.63723025
2024-09-10(二)00:10:26
ID: SzkdS0M (PO主)
>>No.63722661
开摸！
无标题无名氏No.63734650
2024-09-11(三)06:52:22
ID: SzkdS0M (PO主)
教大家一些基本的皮卡丘语:
pikapi=小智
pika pikachu/ pika-pika pikachu=我叫皮卡丘
pi-kachu=皮卡丘(小智等人介绍自己时才会用到)
pikachu-pi=小霞
pika-chu=小刚
pikaka=小光
pipipi=波克比
pi？=（疑问）什么？
PikakaPika=妙蛙种子
PikaPika=杰尼龟/姆克鹰/烈焰猴
pipi-kachu=火箭队
pi-pikachu= (在小智收服到新精灵或者得到徽章时才说)
pi-ka=是、对
Pi-ka-chu？=你还好吗？( 某人物或精灵受伤时才说)
chuuu-pika=铁尾
piika-chuuuuuu=十万伏特
pikaaaaa-chuuuuuu=打雷
pikapikapika... pi-ka=伏特攻击
pipipipipi、chuchughu=电光一闪、高速移动
无标题无名氏No.63739200
2024-09-11(三)16:39:33
ID: SzkdS0M (PO主)
你就说皮卡丘语是不是语言学吧ᕕ( ᐛ )ᕗ
翻了一下，本分区最长串（我翻到的）是899楼，希望我能打破这个记录(`ゥ´ )
无标题无名氏No.63748862
2024-09-12(四)14:35:41
ID: SzkdS0M (PO主)
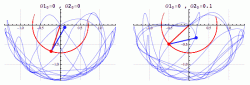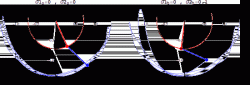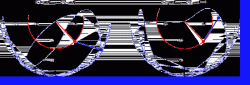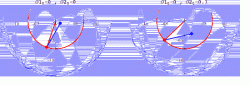
神奇的科学之双摆
双摆，也被称为混沌摆，是一种具有混沌性质的简单动力系统。它可以直观展示所谓的混沌理论：它由一个大摆点和若干小摆点相连组成，其中每个摆都会影响其它摆的运动，因而使整个运动混沌无序，完全无法预测。
而除了运动起来毫无规律之外，混沌摆还有另外一个有趣的特点。他对初值异常的敏感，甚至人手操作的误差也会导致无法实现两次完全相同的摆动。也就是说，输入端微小的差别能够迅速放大到输出端，变成压倒一切的差别。这种现象被称为对初始条件的敏感性。大家熟知的蝴蝶效应便是如此，小小的风吹草动就可能带来难以想象的巨大灾难。
而混沌效应也可以用来解释为什么三体运动问题无法求解。
无标题无名氏No.63755244
2024-09-13(五)07:15:17
ID: SzkdS0M (PO主)
数学冷知识：Google名字的由来
1 古戈尔 = 1 Googol = 10¹⁰⁰
Googol是一个数学术语，指的是1后面跟100个0，该术语是美国数学家爱德华·卡斯纳九岁的侄子米尔顿·西罗蒂所创造出来的，收录于《数学与想象》。
10的古戈尔次方叫 Googolplex (古戈尔普勒克斯)；
10的古戈尔普勒克斯次方叫 Googolduplex (古戈尔双普勒克斯)；
10的古戈尔双普勒克斯次方叫 Googoltriplex (古戈尔三普勒克斯)。
而Google隐藏的意思是能够搜索到浩如烟海的信息。
无标题无名氏No.63764214
2024-09-13(五)23:05:07
ID: SzkdS0M (PO主)
明日份冷知识：金色传说！的企鹅
南极洲发现了罕见的黄金企鹅，何尝不是异色宝可梦呢
在南极洲附近的一个偏远岛屿上，摄影师 Yves Adams 在岛上12万只王企鹅中发现了它。其实黄金企鹅是一只“白化”企鹅，体内不再产生黑色素，所以原本黑色的羽毛变成了黄色或者奶油黄，虽然明亮的羽毛将不利于躲避天敌的攻击，但科学家发现企鹅在择偶时，又会倾向于选择身上含有较多明亮颜色的伴侣，所以黄金企鹅或许在种群中更吃香
无标题无名氏No.63775463
2024-09-14(六)22:52:00
ID: SzkdS0M (PO主)
>>No.63774383
可拉伸单词（stretchable words）
可拉伸单词指的是一种延伸的单词，例如duuuuude、heyyyyy或noooooooo等，这种单词在正式写作中很少见，但在社交媒体中很常见。在口语和书面语中，延伸的单词可以修改单词的含义。例如，“suuuuure”可能表示讽刺，而“yeeesssss”可能表示兴奋。
伯灵顿佛蒙特大学的Tyler Gray和同事对 Twitter 上的内容进行的分析，揭示了人们如何使用可拉伸词。他们开发了一种新的、更彻底的算法来识别推文中的拉伸单词，并使用它来分析随机选择的数据集，该数据集约占2008年9月至2016年12月之间产生的所有推文的10％，总计约1000亿条推文。
研究人员在推文中识别出数千个“可拉伸”单词，包括“ha”(例如“hahaha”或“haaahaha”)，“awesome”(例如“awessssommmmmeeeeeeee”)和“goal”(例如ggggoooooaaaaallllll)。
他们还确定了衡量可伸展单词特征的两种关键方法：平衡和伸展。平衡是指不同字母倾向于重复的程度。 例如，“ha”具有很高的平衡度，因为在拉伸时，“h”和“a”倾向于几乎相等地重复。 “goal”的平衡性较差，“o”重复的次数更多。
伸展度是指一个单词倾向于被拉多长。例如，简短的单词或听起来像“ha”的拟声词具有很高的延伸度，因为人们经常重复多次(例如“哈哈哈哈哈哈哈哈”)。 同时，“infinityyy”之类的常规词的拉伸程度较低，通常仅重复一个字母。
作者补充说：“我们能够全面收集和计算'gooooooaaaalll'和'hahahaha'这样的拉伸词，并在总体拉伸性和拉伸平衡的两个维度上进行映射，同时创造了新的工具，将有助于后续研究的持续发展；并辐射到语言研究，以及其他领域，例如语言处理，扩充词典，改进搜索引擎，分析序列的构造等等。”
无标题无名氏No.63775482
2024-09-14(六)22:53:47
ID: SzkdS0M (PO主)
>>No.63774388
为什么程序的错误叫 Bug ？
据资料记载，早在 1870 年的时候，爱迪生就说过电路的故障可能是 bug 引起的，不过当时还没有电脑这个概念，所以不延伸。
而明确在计算机领域引用 Bug 这个词的是在1947年，程序员葛丽丝·霍普某天工作时发现电脑不能正常运行了，调查很久后才发现是由于电脑内部飞入了一只飞蛾，于是她索性把程序故障，统称为“臭虫”，也就是英文“Bug”。现在在华盛顿的国家历史博物馆中还可以看到这个稿件。
后来，人们逐渐开始用 Bug (虫子) 来称呼计算机中的隐错，而 Debug (除虫) 来称呼修复错误。
无标题无名氏No.63784963
2024-09-15(日)22:29:39
ID: SzkdS0M (PO主)
为什么人拉屎这么慢，动物拉屎很快？
动物拉屎真的很快，几秒到十来秒就完事了。
2017年，一项发表在 Soft Matter 上的流体动力学研究发现，大部分的哺乳动物，无论体型大小，排便的时间都差不多，平均需要12秒。
杨佩良和同事拍摄了大象，大熊猫，疣猪以及狗的排便过程。所有这些动物像人类一样排出圆柱形粪便，虽然体型差距巨大，小至4kg，大至400kg，但排便的时间却一模一样。
而研究表明，动物直肠的一层黏液保证了拉粑粑时间达到最短。体型越大黏液也会更浓稠，这样才能保证粪便排得越快。
那为什么这些哺乳动物拉粑粑时间一样呢？研究者表示原因如下：
1.每种动物的粪便长度均为直肠直径的5倍；
2. 动物由于肠道运动产生的低水平压力是一个恒定值，这与生物的体重无关。
所以无论你大如大象还是小如老鼠，拉粑粑所需的压力都是一样的。撒尿也一样，哺乳动物会花费相同时间来清空膀胱。
刚刚提到的直肠上的那层黏液你知道它的重要性有多大吗？
如果没有这层黏液形成的光滑表层，人需要500天才能排空肠胃。你敢想象拉一次屎居然需要差不多一年半的时间吗！那么人的一生，将会在马桶上度过～
除此之外，研究团队通过收集不同物种的粪便样品，发现饮食方式会影响粪便的密度：食草动物排出的粪便比水轻，而大型食肉动物的粪便则会沉底。
话说回来，这个研究之前是获得了搞笑诺贝尔奖的。她的导师胡立徳和她一起上台受此殊荣。大家应该知道袋熊的方块便便吧，也是杨佩良的研究成果。
如果你觉得你拉屎慢，超过了动物拉屎标准时间，很大程度上和消化系统以及饮食习惯有很大关系。动物的肠道可能更适合快速消化和排泄，以适应它们的生存需求。比如，食草动物需要快速通过消化系统处理大量植物纤维（一般当你排便不顺的时候，你妈都会和你说多吃蔬菜，一个道理……
另外，人类的饮食比较复杂，包括了多种纤维、蛋白质、脂肪和碳水化合物，这可能使得消化过程更加复杂和耗时。而很多动物的饮食比较单一，它们的消化系统可能更适合高效处理特定类型的食物。
如果你嫌拉屎慢，想要获得更快的通便时间，可以换蹲姿，可以换到野外环境，可以改变饮食习惯，可以不要久坐，可以不带手机…也有可能单纯只是便秘了，那就可能需要一些医学方面的治疗了。
毕竟拉屎这件事，十几秒完事还是很爽的…最后，祝各位拉屎愉快~
参考论文：Yang P J, LaMarca M, Kaminski C, et al. Hydrodynamics of defecation[J]. Soft Matter, 2017, 13(29): 4960-4970.
