121. 末世游戏的前期与后期过程太过复杂, 因此这个游戏最多一个月只能玩起来一次,几乎都在周日, 但即便如此也不是每届所有12个学生都能抽出时间来玩, 这是参与游戏的人员会出现空缺和过剩的原因。
122. 北美组织教学用地图系列W-520-500-268-6w-9w-9w-14W4,©赞助年代前1994年, 兰德·麦克纳利公司出版。
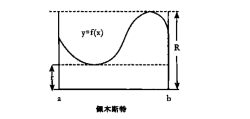
123. 佩木利斯此刻对着因克口述, 后者只需要坐在那里, 指尖并拢, 压在嘴唇上, 笔记都不用记, 就能在下周某个时候一字不差地刻(原文如此)下来, 这个自鸣得意的混蛋。用平均值公式来给每次游戏中的作战队分配百万吨级的东西, 按照“国民生产总值除以军事力量再除以军事力量除以核武器”的比, 比率随着各场末世游戏的变化而变化, 可以让你不必每次都为每支作战队计算出新的比值, 另外还可以让你对结果进行多元线性回归,这样作战队可以为过去慷慨捐献的热核能源得到回报(偶尔华丽的辞藻是哈尔的创作)。这一公式同时可用极值定理证明, 这一定理本身可以通过整个应用微分学里最让人“单元”扭曲的玩意儿自证, 但我现在能看到哈尔已然一脸痛苦, 所以我们还是尽量简单点,虽然如果你有兴趣的话, 这一切其实很有意思。假设你有每支作战队“国民生产总值除以军事力量再除以军事力量除以核武器”的比率数据。我们给作战部队分配的数量要接近过去分配的精确的平均值。这个精确的平均数叫作“平均值”, 这肯定让我们能笑一笑, 考虑到语境中的敌对状态。那么让我们用A代表作战队不断波动的比的平均值, 也就是不断变化的最初百万吨级平均值。我们要找到A并给予作战队精确的A百万吨。怎么做, 这很优雅, 你需要的只有两个数据: 比率最高点和比率最低点。这两个数据(原话)被叫作 A作为平均值的 cn-n函数里的极值, 顺便说一下。设f是区间[a, b]中的一个连续的非负函数(即比率),而这个区间即最低比率和最高比率之间的差, 诸如此类。是不是越解释越晦涩(原话)了? 因克看着我的样子好像能让黄油冻住一样。很难搞明白什么是假设的, 什么是需要解释的。我在尝试尽我最大可能表达清楚(原话)。现在他看我的样子好像我跑题了。你干吗不把那什么玩意儿递回来呢, 因克特。这样我们有了f, 还有区间[a,b]。这样r和R就是函数f(x)在[a, b]区间内的最小和最大值。看看高度r和高度R在图中区间[a, b]上形成的矩形, 就叫这张图表“佩木斯特”好了:
